こんにちは。tokuです。
今回はExcelで分析ツールを使わずに重回帰分析をしてみたいと思います。
Excelで分析ツールを使ったものの結果がしっくりこない場合、説明変数が多くて分析ツールを利用できない場合などに使ってみてください。
偏回帰係数(説明変数の係数)を求めてみよう
重回帰分析のサンプルコードを具体例を通して紹介します。
今回は下記のエクセルファイルを用います。
私もそうですがネット上のファイルをダウンロードして開くのに抵抗がある方もいると思うので、適宜スクリーンショットを用いて説明します。
まず、予測したい変数である目的変数と予測に使う変数である説明変数の実績値をExcelで整理します。
今回の用いるデータは「重回帰_使用データ」というシートに入っています。
目的変数としてある店舗でのアイスの年間総売上高[百万円]、説明変数として気温[℃]、湿度[%]、天気[ダミー変数:晴れ=0、雨=1]のデータを用いています。(図1)
説明変数ではないですが、重回帰の定数項用に1のみのデータも作っておきます。目的変数のデータの範囲は”重回帰使用データ!A3:A101″、説明変数と定数項用のデータの範囲は”重回帰使用データ!B2:E101″です。
“重回帰使用データ!”はExcelのシート名を示しています。

図1 目的変数と説明変数
次に、偏回帰係数(説明変数の係数)と定数項を求めていきます。重回帰分析の具体的な計算・証明に関しては本記事では割愛します。今回説明変数の係数が3つ、定数項1つで4つの解が出てきます。図2のように4つのセルを縦方向に選択した状態で下記のコードを入力してEnterを押します。結果は「重回帰_結果」というシートに出力しています。
=MMULT(MMULT(MINVERSE(MMULT(TRANSPOSE(重回帰使用データ!B3:E101),重回帰使用データ!B3:E101)),TRANSPOSE(重回帰使用データ!B3:E101)),重回帰使用データ!A3:A101)

図2 偏回帰係数と定数項の計算
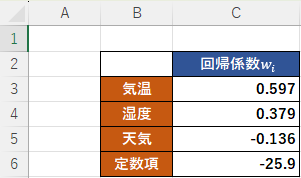
各説明変数の偏回帰係数と定数項が求まりました。(図3)

図3 偏回帰係数と定数項の計算結果
偏回帰係数の妥当性を確認しよう
ここでは詳しく説明しませんが、重回帰分析を行った結果が妥当であるか確かめる方法はいくつかあります。
今回は目的変数の実績値と偏回帰係数、定数項、説明変数から算出した目的変数の予測値が概ね一致しているかを見て妥当性を判断しましょう。
図3の偏回帰係数と定数項から目的変数の予測値は次のようになります。
[売上高]=0.597×[気温]+0.379×[湿度]-0.136×[天気]-25.9
※係数はここでは簡単のため有効数字3桁とした。
Excel上で目的変数の実績値と回帰による予測値を図4のように並べてみました。図5のように予測値と実績値の散布図は概ねy=x上に乗っており、予測精度が良いと思われます。これらは「重回帰_結果」のシートで行っています。

図4 予測値の算出

図5 予測値と実績値の散布図とy=x
決定係数を求めてみよう
決定係数\( R^2 \)は回帰式が実際の目的変数をどの程度説明できているかを示しています。
詳しい説明はしませんが、目的変数を\( y_i \)、その平均値を\( \bar{y} \)、回帰の予測値を\( \hat{y}_i \)とすると、\[ R^2 = \frac{ \sum_{i=1}^{n} \left( \hat{y}_i – \bar{y} \right) ^2}{ \sum_{i=1}^{n} \left( y_i – \bar{y} \right) ^2 } \]となる。
Excel上で計算すると図6のようになります。順序立てて決定係数を求めています。

図6 決定係数の算出
最後に
今回はExcelで分析ツールを用いずに重回帰分析を行う方法を紹介いたしました。
Excelでの重回帰分析は分析ツールを用いた記事が多いのですが、分析ツールを使わない方法はあるかもしれませんが、なかなか見当たりませんでした。
説明変数が多くて分析ツールを使えない場合など特殊なケースになると思いますが、本記事を参考にして重回帰していただけると幸いです。